CONCEPTS OF RELIABILITY ENGINEERING (RE)

FOR THE COMMON MAN

Dr. I. Achyuta Rao

“Do not have the apprehension

That RE is beyond your comprehension”

—An unknown scientist

Reliability engineering (RE) is the ultimate in engineering techniques. It is applicable to all branches of engineering and technology. It leads to the “state of absolute perfection” in the relevant fields. If proper care is exercised, it is applicable to bioengineering and biotechnology also. It is extendable to the fields of surgery, medicine and pharmacy. The common man, as the user, is the prime beneficiary of RE techniques, hence the need for publication of this article in this journal.

We buy many household articles in the market. They fail to work immediately after bringing them home or after a few days or months of usage. We have to get them repaired or replaced. It becomes a nuisance some times. An item does not work when we want to use it. Even if it works for some time, it fails at the most crucial moment. That means, the item does not have adequate “RELIABILITY”. The concept of warranty/guarantee arises, only out of this unpleasant experience.

On the other hand certain items work without fail for hours or even days and months. In extreme cases they work “failure free” for years at a stretch. We reach a sublime state or heaven. Such items are stated to have high reliability (R). The common man wants high R of all items, to lead a pleasant and peaceful life. That is why the craze for “foreign goods” arose, of late.

(During World War II cheap Japanese goods flooded the Asian market. They used to fail miserably and people used to call them “Japanese Products” meaning of low reliability. After the war, Japan developed the RE field so much, that their products are the best and most reliable items today. Now the Chinese goods have flooded our markets).

Some items are repairable or maintainable. After repair or maintenance, they continue to work “failure free” for months or years. I do not wish to dwell on this aspect here but cover the generic term R.

Definition of Reliability (R)

Then what is Reliability? It is a concept statistically defined as “the probability that an item performs its intended function, under stated environmental conditions, for a given time of operation”.

Notionally, if the item is not expected to fail ‘at all’ during that specified time, the R is I. If it is sure to fail during that time, the R is O. The actual (probability or) reliability value lies between these extreme values 0 and 1.

The R of an item depends essentially on its failure rate (F). If the failure rate is low, reliability R is high and vice-versa. In order to have high R, the item should have low failure rate, by design and careful manufacture. The scientific expression for reliability is

R =e ^-Ft where, “t” is time of operation. In fact, R falls off exponentially with increase of time. Note that the fall is not due to wear and tear with time (since it occurs even if the F is constant). Of course wear and tear cause increase of F, which causes lowering of R., as explained earlier.

Failure Rate (F)

Failure rate (F) is the reciprocal of the time an item or component takes to fail, on an average. If it takes ten minutes to fail, F is 1/10 per minute.

Probability Concepts

The failure rate (F) is an average value taken over several tests. The item may not fail at the average value of time recorded. It may fail at any time before that or after that, hence the need for introducing probability concepts.

If an item contains two components whose failure rates are FI and F2, the reliability R of the item is the product of component reliabilities

R=e^-F₁^t x e^-F₂^t = e^-(F₁^+F₂^{) t}

It is obvious from the above that the failure rate of the item is the sum of failure rates of the two individual components, because anyone of the two components may fail at any time.

If an item contains a number of components (say 10) the failure rate of the item is the sum total of the failure rates of all the (10) components. So, if the number of components is larger, the failure rate of the item is higher and its reliability lower.

One understands, that the simpler the item (containing a smaller number of components), higher the R and for a complex item (containing larger number of components) lower the R.

New and un-established technologies have high failure rates and hence low R values. Once the technology is perfected, the failure rate becomes lower and R value higher.

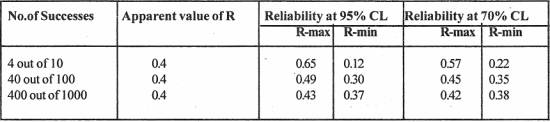
Number of Tests for R-Estimation

A suitable number of an item is taken for (performance) tests (under stated environmental conditions) and the number that passed the test is recorded to estimate R.

If 4 out of 10 tests resulted in total success, the R is 0.4

If 40 out of 100 tests resulted in total success, the R is still 0.4 (but with greater confidence level.

If 400 out of 1000 tests resulted in total success, the R is still 0.4 (but with still greater confidence level (Partial success is not considered for R estimation).

Confidence Levels (CL)

Thus the statistical confidence levels are introduced to bring in more realistic estimation of R.

If we fix our confidence level at 95%, the above three sets of results give different values of R. In fact, one upper limit and one lower limit are given for each set of results indicating a range of values based on the probability.

If we fix our confidence level at 70% the three values of R-limits are closer, as seen in the above table. For both the CL’s, R-max and R-min are closer in the case of large number of tests. They tend to merge at 0.4, when the number of tests tends to 00.

The lower limit is the criterion for accepting the item based on tests. (100% confidence level is purely notional but not practical).

This brings to our appreciation that the number of tests on an item (or the number of identical items tested) should be as large as possible to get a realistic value at adequate confidence levels. It is up to us to specify the CL depending on the situation and our requirement.

During my short visit to United States, I happened to study a number of research papers published in the fields of medicine and pharmacy, based on as small a sample size or number of tests) as 15 to 25. It is grossly inadequate to give any reasonable confidence level, say 60 to 90%. Often, the earlier conclusions based on limited tests were reversed based on results of more extensive tests.

Concern for Reliability

Suppose a complex system like a Guided Missile or Satellite Launch System (one shot or non-repairable systems) consists of 6 sub-systems.

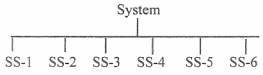
Failure of anyone sub-system will cause failure of the entire system. The reliability RS of the total system is the product of the individual reliabilities of the 6 sub-systems.

R_s= R₁.R₂.R₃.R₄.R₅.R₆

For example,

Rs = (0.9) (0.9) (0.8) (0.8) (0.9) (0.8) = 0.37

If each sub-system has 4 assemblies, the reliability R_i of the sub-system is the product of the individual reliabilities of the 4 assemblies.

R_i = a₁.a₂.a₃.a₄ where a_i is the R of an assembly. For example,

R_i = (0.97) (0.97) (0.98) (0.98) = 0.9

Similarly, if each assembly has 5 sub assemblies, the reliability a_i of the assembly is the product of the individual reliabilities of the 5 sub-assemblies.

a_i = r₁.r_2..r₃.r₄.r₅ where r_i is the R of the subassembly. For example,

a_i = (0.996) (0.996) (0.996) (0.996) (0.996) = 0.98

Thus we can go further down to individual components.

A complex system like a Guided Missile may have one million components. Imagine the probability of the system failure due to failure of anyone of the million components. This poses the questions; a) how do we go about designing for the specified system reliability R_s and then achieve it in practice? b) how do we evaluate the R-design and then demonstrate the achieved reliability R_s?

Redundancy

In the case of highly critical sub-systems/components or where the specified reliability cannot be achieved in practice (when we reach the ultimate), redundancy is introduced on the principle of parallel circuits.

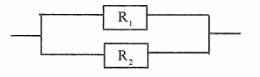
R = 1- (l-R₁) (l-R₂)

Where I-R₁ is the probability of upper block failure

I -R₂ is the probability of lower block failure

(l-R₁)(l-R₂) is the probability of both of them failing.

R is the probability of both of these not failing (at least one will work)

If R₁ = 0.7 and R₂ = 0.8, R is 0.94, higher than both R₁ and R₂.

“RE” Techniques

R-Apportionment to sub-systems, assemblies and sub-assemblies

R-Design evaluation methods

R-Test methods

- Destructive and Non-Destructive tests

- Time terminated tests

- Failure-terminated tests etc.

Fault- Tree Analysis

Statistical sampling techniques

R-Block diagram

R-Demonstration

R-Growth models etc,

are beyond the scope of this article. However, the basic concepts of interest to the common man are indicated.

How To Make A Reliable Item/System

1) Make the item simple. (Minimise the number of components)

2) Use good quality materials (follow national and international standards

3) Use only established technologies

4) Use components with low failure rates (follow various standards)

5) Carry out extensive tests to eliminate

a) Design deficiencies

b) Defective components

c) Defective and non-standard materials and improve intrinsic reliability

6) Keep the operational environmental conditions in view while choosing the materials, processes and components

7) Introduce redundancy wherever essential

8) Train the workers to high-skill level

9) Educate the workers to appreciate high quality requirements

10) Motivate the workers for full participation, devotion, dedication and responsibility

11) Educate the workers on the concepts of RE and their appreciations

One should remember the SAYING

For want of a nail, a shoe was lost

For want of a shoe, a horse was lost

For want of a horse, a rider was lost

For want of a rider, a battle was lost

For want of a battle, a war was lost

Tasks Involved

However, it is not an easy task to

- Specify appropriate reliability R_s to a complex system

- Design the system for the specified R_s

- Apportion sub-system, assembly and sub-assembly reliabilities (R_i, a _i, and r_i)

- Achieve them in hardware fabrication-Demonstrate them by proper tests

- Maintain them in bulk manufacture

- Prove them by conduction of sample tests

- Finally prove the system reliability R_s in tests.

“The grass is always greener on the other side of the fence” said the Jackass, as it stretched its neck in the attempt to reach it.

Oscar Wlilde said: “Most men are other people. Their thoughts are some one else’s opinions, their lines a mimicry, their passions a quotation.”

We should remain true to our tradition and the ethos of the Indian culture. Yet we may accept certain good features of a foreign culture. Infact that is the beauty of our Indian culture which is a composite and our revolving culture. Our motto should be ADAPT but not ADOPT.

Back